1. Home
2. categories
3. fixed-point-math
4. Testing the Accuracy of libmathq15 on the PIC24

For a quick primer on libmathq15, check out How Fixed-Point Math Works.

Intro

Recently, I have been curious as to the accuracy of libmathq15 over
the entire sine range, which is 0 to 65535 for trigonometric functions and -32768 to 32767 for the standard Q1.15 functions.  Realizing quickly that this range is very reasonable to check, I went to work using the PIC24 simulator to get my results.

This is a long post, grab a cup of coffee!

Version?

The accuracy tests would not be complete without some sort of version information.  All testing was run against git commit hash '5519ce5f96f2daa412882503473527f218e3f31e' on github.

From Simulator to File

The first thing that I want to do is save data to a file.  I don't want to copy/paste 65536 entries into a file from the console.  Fortunately, the device simulator that comes with the MPLAB X environment has the option of exporting 'printf' statements to the console or to a file:

1. File -> Project Properties
2. Under 'Categories', click 'Simulator'
3. Under 'Option Categories' drop down, click 'Uart1 IO Options'
4. Check the checkbox, choose your output type (console or file)
5. If 'file' is the desired output, choose a file name

In the file that needs to contain printf statements, you need to include as well.

Quick note about simulation, if you want to repeat this testing, all files are in github, but I would recommend running it on the silicon and using the UART to send the data back into PuTTy or something similar.  The simulation took entirely too long for my liking and the hardware probably would have blown the sim out of the water.

The Program Unfolds

The First Draft

We are going to use float types and math.h as our 'standard' by which to judge error.

For the remainder of this section, I am going to use the testing for the sine function as the 'sample', but you should know that the results will include multiplication, division, etc.

For the sine function, we will start at a fixed-point angle of '0' and convert that to the floating-point equivalent.  We will then execute both fixed-point and floating-point sine functions.  Finally, we will scale the floating-point value to fixed-point to determine the error in 'bits'.

This thought process resulted in the below program:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int main(void){
    /* print column headers */
    printf("float_val, fixed_val, float_sine, fixed_sine, fixed_err");

    q16angle_t q16_angle_num = 0;

    while(q16_angle_num < 65535){
        /* convert fixed-point to radians */
        float float_val = (float)q16_angle_num * 2.0 * 3.14159 / 65536.0;

        /* calculate sine of float and of fixed */
        float float_sine = sin(float_val);
        q15_t fixed_sine = q15_sin(q16_angle_num);

        /* calculate the error in points */
        float fixed_err = (float_sine * 32768.0) - (float)fixed_sine;

        /* print relevant values to the console */
        printf("%f,%d,%f,%d,%f\n", 
                (double)float_val,
                q16_angle_num,
                (double)float_sine,
                fixed_sine,
                (double)fixed_err);

        q16_angle_num++;
    }

    while(1);

    return 0;
}

Our goal is to generate a nice CSV file which can easily be parsed by most plotting tools, including gnuplot.

The Wrinkles

While running this program, I noticed that it was taking a really long time and I decided to take a peek at the results.  I saw a repeating pattern, the program was continually 'resetting' at the beginning of program execution!  What was going on here?

Wrinkle 1: The Watchdog Timer

There is a function of the microcontroller that exists solely to reset the microcontroller periodically if it is not 'serviced': the WatchDog timer.  The job of the watchdog timer is to reset the microcontroller when the code goes out of bounds due to anything from cosmic rays to bad programming practices.  In many cases, you might not even notice a watchdog timer reset.  I have seen it happen on an assembly that was spinning at 50000 RPM and the only way that I knew that something odd was happening was an odd 'click' every now and then.  Simply insert the below line at the top of your program and the watchdog timer should be disabled.  Alternatively, you could add a 'ClrWdt()' call to your while loop and get the same effect.

1

#pragma config FWDTEN = OFF

After inserting the configuration bit that turns the watchdog timer off, all went well.  Our program takes several minutes to execute - maybe half an hour?  Only after it finished did I stop to think about all of the processes that are working together here - PIC24 machine instructions running on a device simulator which is running on Java, then on my hardware.  No wonder it took several minutes.  If you decide to run this yourself, hit 'go', make sure it is working, then go get lunch.

Wrinkle 2: printf Integer Formatting

It turns out that the 'printf' function used always sees 16-bit numbers as signed, so when the number is of type uint16_t and is a value of '32768', printf will output this as '-32768'.  This inspired us to do a 'float' conversion right in the printf to keep the float and fixed point comparisons on the same horizontal scale.

Wrinkle 3: No 'equivalent' Column

Our program above did a conversion just before an error check, but there was no conversion archived.  It would be convenient to have the fixed-point scaled value archived in the CSV file so that we can overlay the two plots during the analysis stage.

The final program executed is below, which is very similar, with the 'wrinkles' ironed out:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

int main(void){
    /* print column headers */
    printf("float_val, fixed_val, float_sine, fixed_sine, scaled_float, fixed_err");

    q16angle_t q16_angle_num = 0;

    while(q16_angle_num < 65535){
        /* convert fixed-point to radians */
        float float_val = (float)q16_angle_num * 2.0 * 3.14159 / 65536.0;

        /* calculate sine of float and of fixed */
        float float_sine = sin(float_val);
        q15_t fixed_sine = q15_sin(q16_angle_num);

        /* scale the floating-point to fixed-point for comparison */
        float scaled_sine = float_sine * 32768.0;

        /* calculate the error in points */
        float fixed_err = (float_sine * 32768.0) - (float)fixed_sine;

        /* print relevant values to the console */
        printf("%f,%d,%d,%d,%f\n", 
                (double)float_val,
                (double)q16_angle_num,
                (double)float_sine,
                (double)fixed_sine,
                (double)scaled_sine,
                (double)fixed_err);

        q16_angle_num++;
    }

    while(1);

    return 0;
}

We will execute similar programs for the other functions under test as well.  There are some functions that require two parameters.  When this is the case, we will simply choose a set of values to run instead of attempting to run all possible input values.  We are comfortable with this approach since unit testing covers the edge cases.  Here are some quick details:

• q15_mul() - tested with 24567 and -1024 as the multiplier
• q15_div() - tested with 24567 and -1024 as the dividend
• q15_add() - tested with 24567 and -1024 as the adder
• q15_abs() - tested full range
• q15_sqrt() - tested full range
• q15_sin() - tested full range, 8-bit table
• q15_cos() - tested full range, 8-bit table

Analysis

Finally, we have data!  My less-than-humble opinion on data is that if you can't see it, then you probably don't understand it.  Humans are visual creatures above all else, so plots are extremely important to gaining a full understanding of any data set.  You can find the datasets on github.

Having said that, gnuplot is my favorite plotting tool for quickly plotting nice little graphs from CSV files.  All plots shown were generated using this a gnuplot script.  To execute the script, you must have gnuplot installed.  Navigate to the directory with the data and the script.  On the command line, type:

gnuplot gnuplot_script.txt

All of your PNGs will be generated from the data.  There are lots of gnuplot tutorials out there, but feel free to copy/paste mine.  Remember, when you are customizing the script, the order of the commands matters!

Results

The results are specific to the operation, so we will break them out here.  This is a summary of plots created.  The full data set can be found on the github repository.

Multiplication

The q15_mul multiplication function is dead-on across the range tested.  As we are using multiplication hardware available on the device, this is no surprise.  Errors are less than 1 bit.

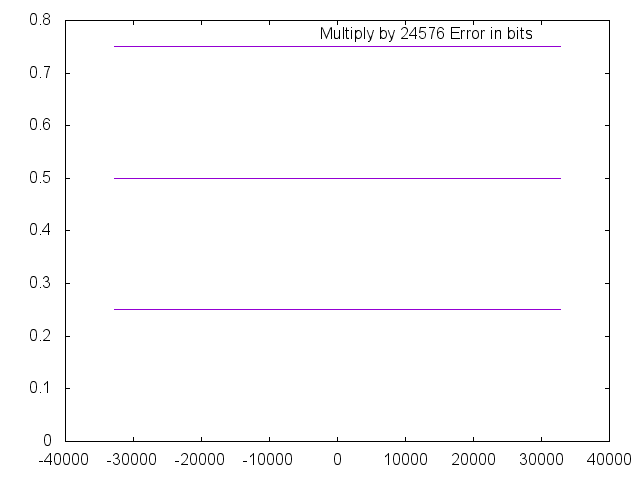
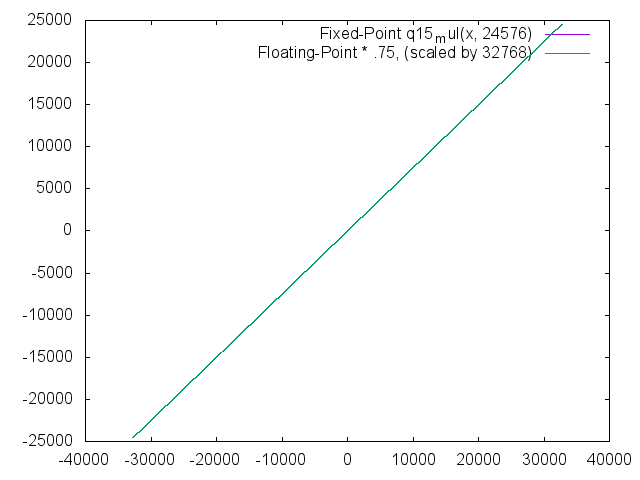
Division

The q15_div function operates perfectly until the magnitude of the divisor (denominator) becomes equal to or greater than the magnitude of the dividend.  As mentioned in the past, in Q1.15 math, the magnitude of the divisor MUST be less than the magnitude of the dividend OR the result will saturate.

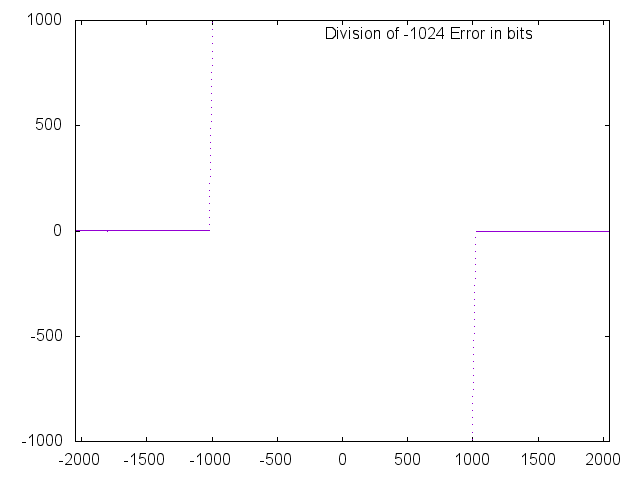
Note the saturation (below) when the magnitude of the divisor becomes less than the magnitude of the dividend.  On all other values, the error is less than 1 bit.

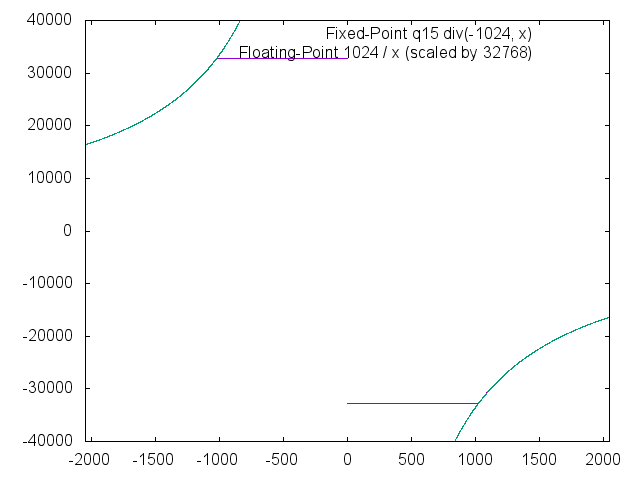
Addition

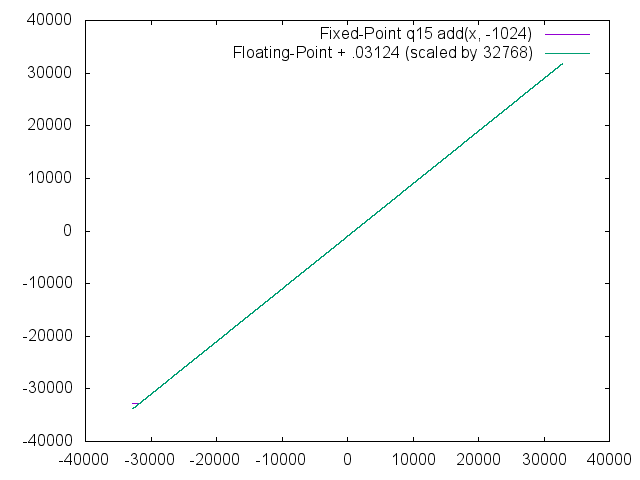
To test addition, we simply add a static number to every possible number.  In this case, that number is '-1024'.  Note that the error is 0 everywhere except in the region in which the result saturates.

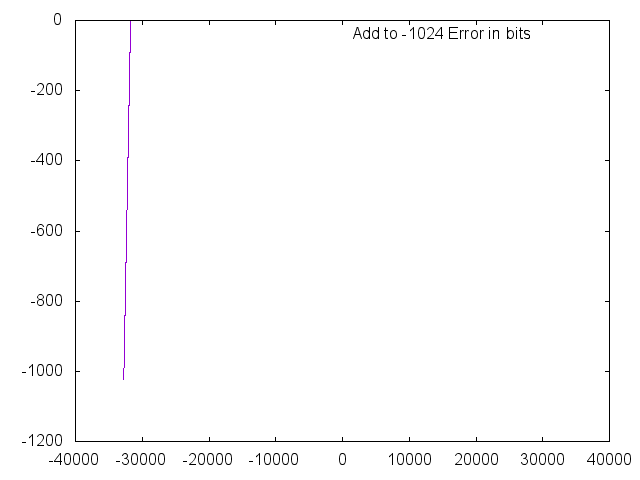
In the overlay, you can see a small 'tail' at the bottom left where the result saturates.

Absolute Value

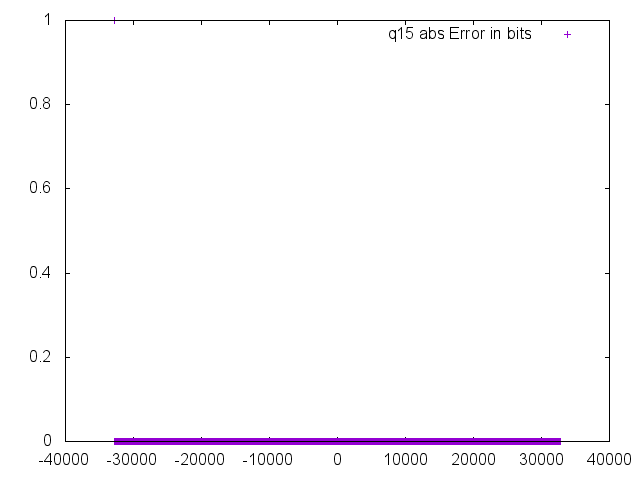
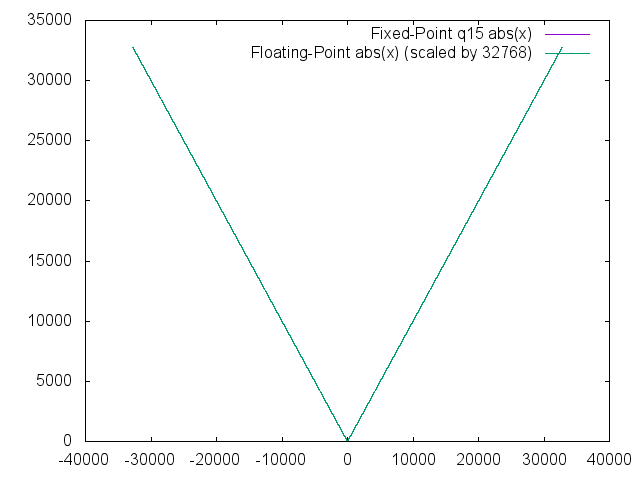
No surprise, the absolute value function displays no error relative to the floating-point function over the entire range.

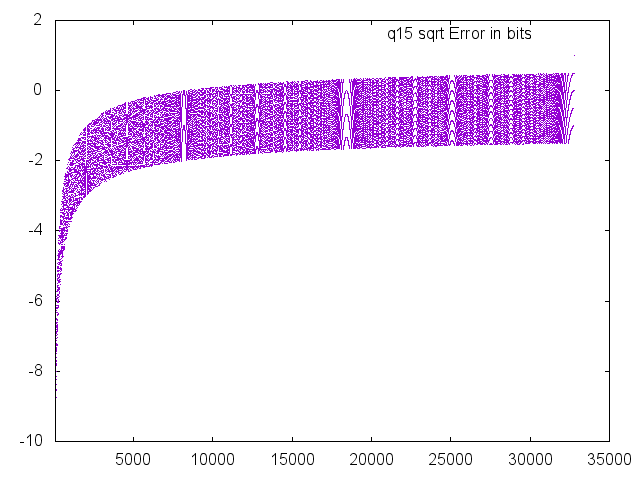
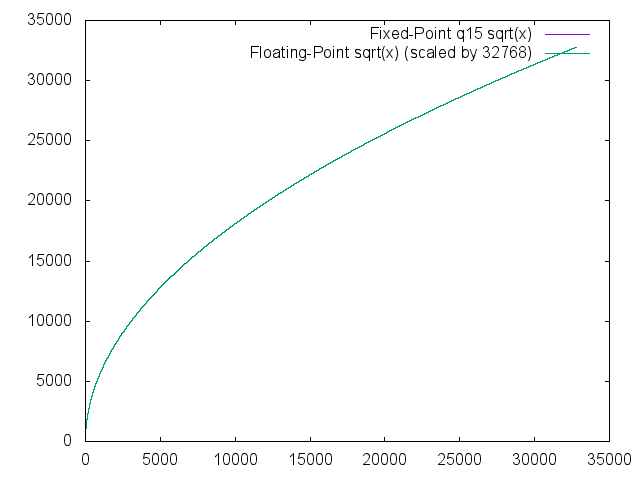
Square Root

The Q1.15 square root is very accurate except when the number is very small.  I have included two plots of the error, one that runs from 0 to 100 and the other that runs from 101 on.  Note that the error below an input of \~40 is greater than 20 bits.

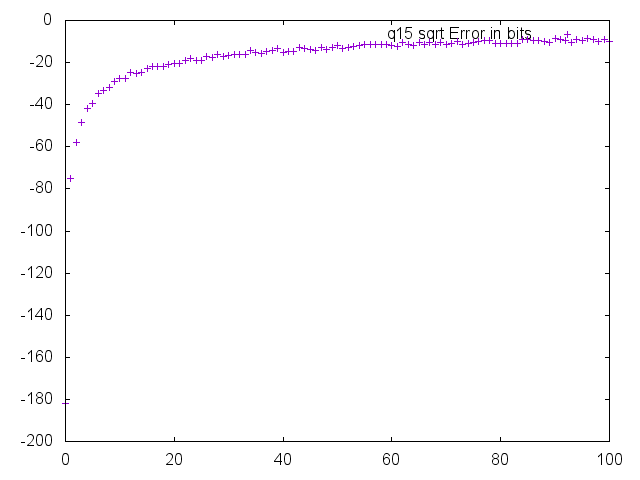
The error quickly drops to less than 10 bits and stays below 2 bits for the majority of the range of the function.

Sine

Just for clarification, this code was executed on the '8-bit' table, which is the highest resolution table.  The lowest resolution table is the 4-bit table, which likely has much worse errors.

The error in every odd input were observed to be worse than the even data points.  On closer inspection, it appears that the odd and even numbers that are adjacent (0 and 1, 2 and 3, etc.) are actually the same number across the range.  Regardless, the error is very low - certainly good enough for the majority of applications.  Future library improvements will likely target this function first since the previous functions have all behaved with lower error

On the overlay, you still can't even see the two different data sets.

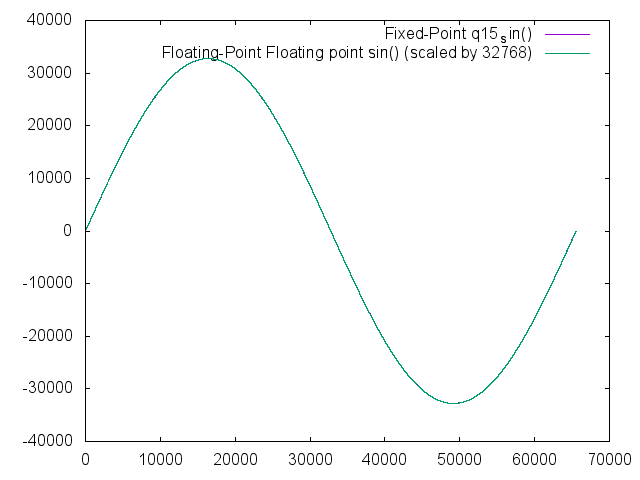
Fast Sine

The fast sine is simply a lookup table within the code with no interpolation.  As a result, it gives up accuracy for the sake of speed.  Fortunately, this is often plenty of accuracy to run a motor or meet other functional requirements.

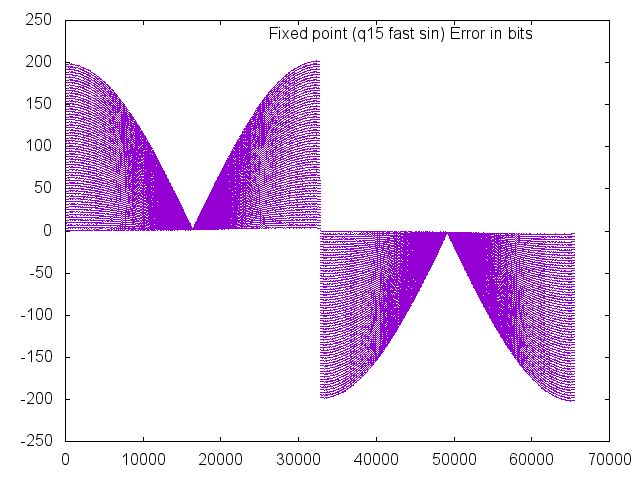
Since the lookup table is only implemented for 90 degrees and calculated for the other quadrants, it may be more appropriate to just look at the first quadrant.

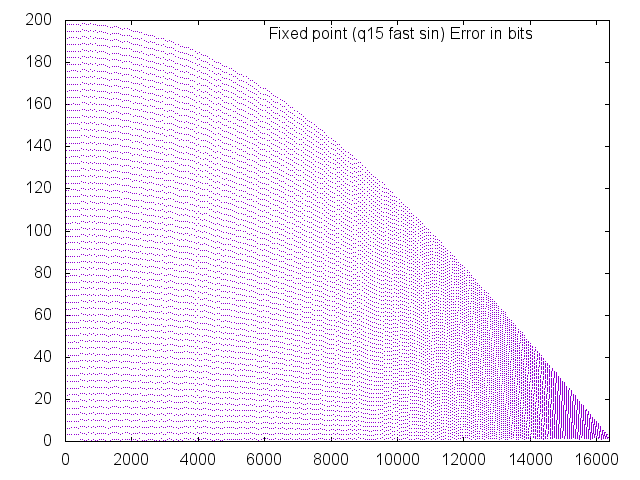
Even with this amount of error, the overlay still looks quite adequate for most tasks.

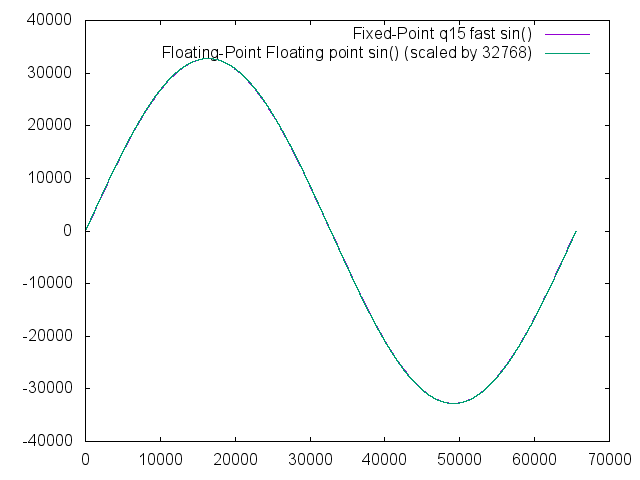
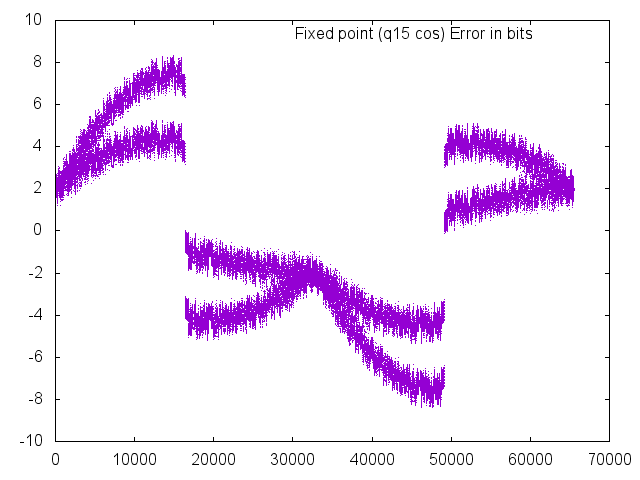
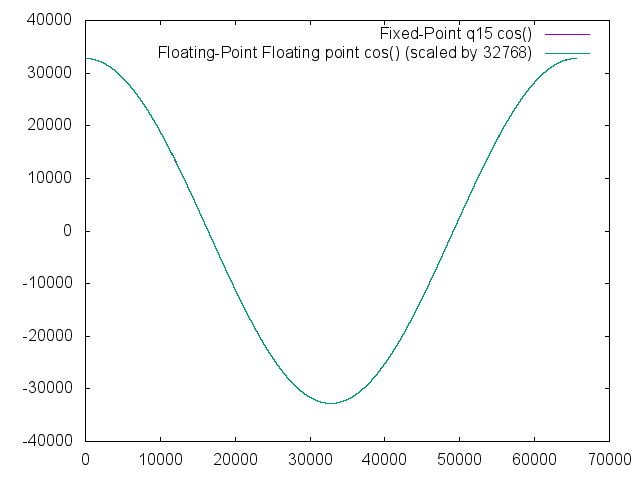
Cosine

Results look very similar to the sine function, just shifted 90 degrees.  Again, small room for improvement, but the results are definitely very usable in the majority of applications.

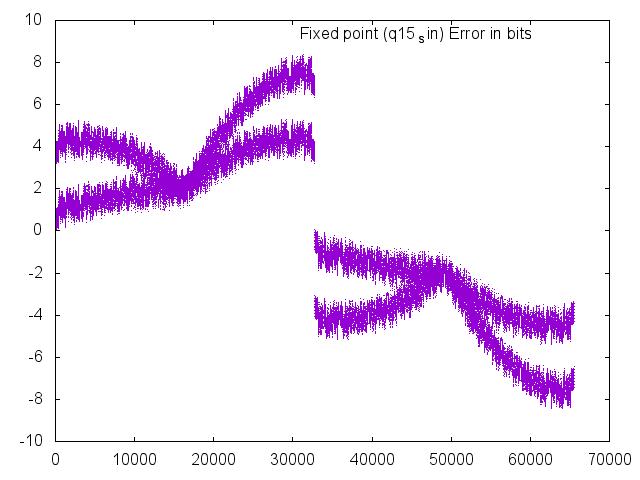
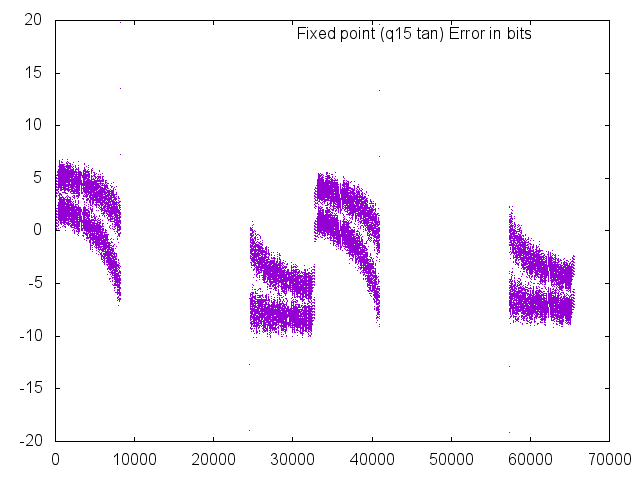
Tangent

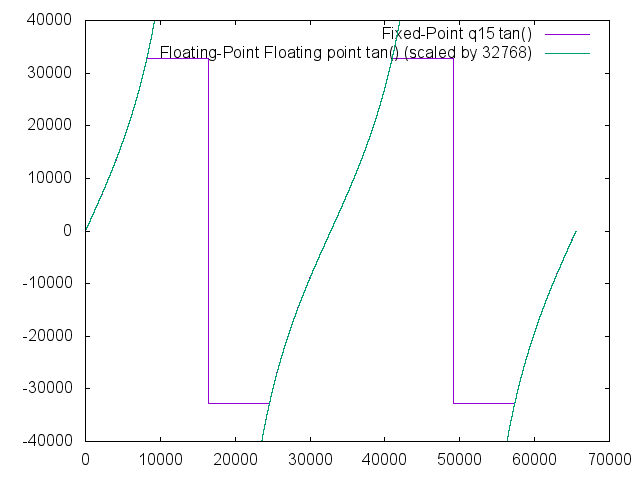
A tangent function is included in the q15 library for completeness, but its functionality is severely limited by the inability of the format to represent numbers greater in magnitude than 1.0.  In the ranges of 57344 (-45 degrees) to 8192 (45 degrees) and 24575 (135 degrees) to 40959 (225 degrees), the results are valid with errors never going beyond +/- 10 bits.

The below plot shows the saturation that occurs as a result of the Q1.15 format, which causes the large errors.  Note that the overlay is nearly perfect in the valid regions.

The other two 'fast' trigonometric functions were omitted from this study since they will show similar results to the fast sine.

Conclusion

On the whole, the library is fully functional on the XC16 platform.  There could be some other details addressed and there is room for improvement, but the library is ready for production as is.

• Previous Article
• Next Article

• Previous in fixed-point-math